Bamboo C.O.R.P.S.
Elegant Bamboo Models of the Polyhedral Solids
Welcome!
Build your own set of 3-D Polyhedrons - Tessalations of the Sphere known as polyhedra with one of our bamboo kits. The polyhedron models on the right are all made with natural bamboo.
Bamboo models are far superior to paper or cardboard models of polyhedra since they allow viewing of all sides. These durable models of the Platonic and Archimedean solids make great displays, especially as ceiling or wall hangings! The natural look of bamboo turns the contructions into elegant decorations that look stunning in any living space, office, or educational environment.
Paper Models of Platonic and Archimediean Solids, or "Polyhedra" are great, but Polyhedron Models made from bamboo are better. Paper nets of polyhedra folded and glued are readily available - here are links to where you can find them. Consider however elegant, artistic, durable strong and permanent construction with Bamboo and the FOCUS method, vs. fragile, cheap looking, opaque, (and so not "nestable") and less than unique (Every-body has done them) polyhedrons made with paper nets. Construction time is similar.
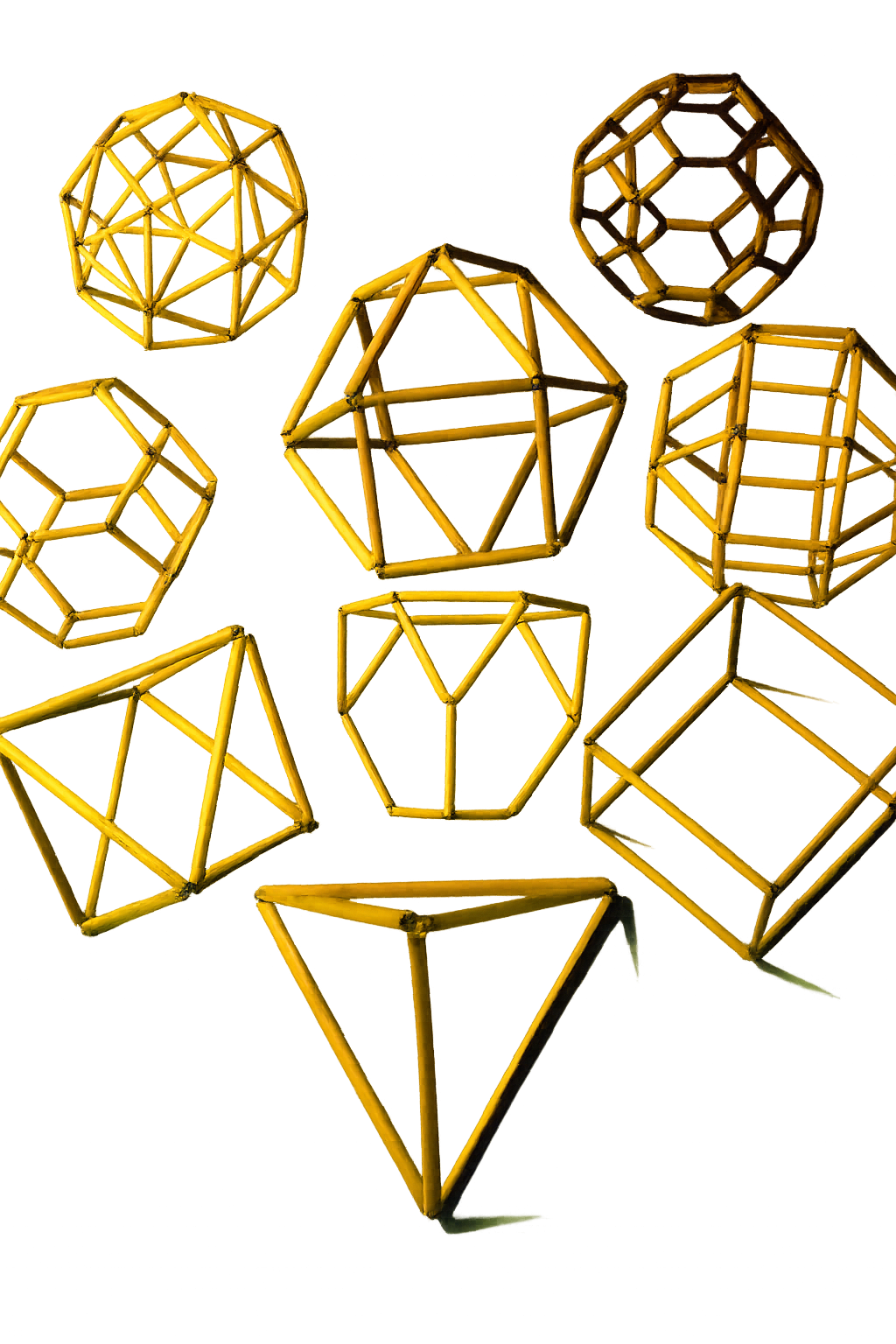
Bamboo is an excellent construction material
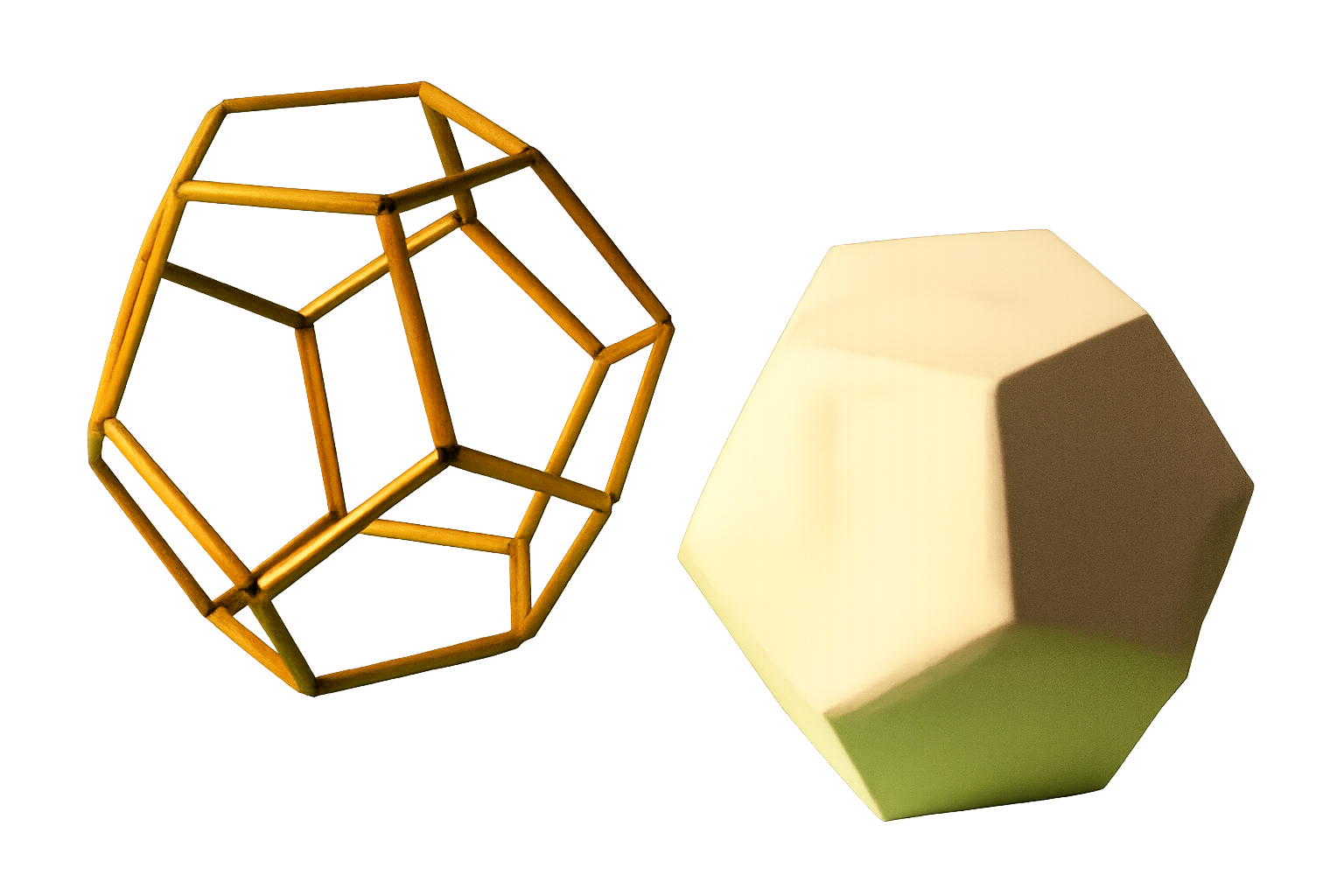
The BambooCORPS will make available and promote the use of those smaller pieces of bamboo (often left in the field to decay or burned) for creative expression. Though we promote our pre-made kits for regular polyhedra, this bamboo and this method of construction lends itself to other creative uses. We will strive to make segments of bamboo available and provide instruction for effective use of it. We anticipate an application in kinetic sculpture, tensegrity modeling, architectural (geodesic etc.) studies, modeling of chemical compounds with accurate bond angles and distances etc. Use your imagination, then let us be your source for these wonderful, beautiful , surprisingly rigid and durable segments of wood that Mother Nature so conveniantly supplies with a hole pre-drilled down the middle!
Are you interested in Platonic and Archimedean Solids?
Join the Bamboo C.O.R.P.S.!
Enrollees assemble stunning 3-D models of the regular polyhedra that are durable enough to be roughly handled and dropped! They will “join the bamboo” using nearly invisible yet almost indestructible instant (No “drying” time!) bonding between multiple sides.
The open corners, (or “vertices”) greatly facilitate nesting, building one polyhedron inside of another polyhedron. Nested polyhedra demonstrate inter-related properties between two or more polyhedra. These properties could not be realized with commonly performed cardboard or paper models of polyhedra.
Most surprising is that the construction is easier and less time consuming* with greater durability and artistic appeal than with paper or cardboard models of polyhedra. Perfect for Science Fairs Project, Math or Geometry Project, Classroom Demos, Hands-on Children's Museum display, and adaptable for use in Architctural modeling for Geodesic construction, etc. etc!
Background Information
The structures found throughout this site were known and revered by enlightened ancients. Those known to have been described by plato have the additional constraint that all faces as well as sides and vertices are identical. There are only five such. Archimedes gave his name to 13 additional structures, all with identical sides and vertices, but with variable faces- triangles, pentagons, squares etc. joining together to tessellate the sphere. These structures are now known as platonic and archimedean solids, and are part of the more general set of polyhedral solids.
The polyhedral solids are essentially the tessallations of a sphere. Regular tiling of one or more various side number polygons that completely fill a planar surface in a simple repeating pattern defines a tessalation. If one adds the constraint that all sides shall have equal length the pattern is designated as “regular”. In many cases simply reducing the number of polygons meeting at a vertex or even reducing the number of sides of one of the polygons results in the tessalation of a sphere rather than the plane. It is not surprising that decreasing the elements causes an angulation that when repeated gives a curve. What seems astounding is that the curvatures so formed in any direction should come back and co-incide where it started, thus evenly and completely enclosing a sphere. The eureka moment of delight in fully grasping this is only realized when one actually starts with planar polygonal shapes and watches the three dimensional shape seem to erupt as the planar polygons are joined in the process of construction.
Links
Big Bamboo Company - Our MOTHER company, the exclusive producer of our natural bamboo!
We grow it, process it and sell direct to youThe Big Bamboo Company has developed a special heat treatment process that produces a natural glaze finish on their products. Products include GIANT bamboo building timbers, uncommon naturally BLACK bamboo, and BLUE henna bamboo. Featuring their "Good Neighbor" Privacy fence made with beautiful Tonkin bamboo. Live plants also shipped anywhere. With no "middle-man" you won't likely get better service or price anywhere else. Delighted clients include the Smithsonian Institute, The Bellagio, and the Alexandria Zoo, and yes- the BambooCORPS!
GeometryCode Sacred Geometry IS Bruce Rawles. The information and inspiration needed to create the BambooCORPS came largely from the detailed and awe-inspiring pages of his website- (we bought and treasure his book also!) He would be the Metaphysical FATHER of our hopeful little endeavor.Anyone with ANY interest at all in the inherent beauty of these structures will be fascinated by the offerrings of this High Priest of Geometry! Examine this quote from his home page:
In nature, we find patterns, designs, and structures from the most miniscule particles, to expressions of life discernable by human eyes, to the greater cosmos. These inevitabley follow geometrical archetypes, which reveal to us the nature of each form and its vibrational resonances. They are also symbolic of the underlying metaphysical principle of the inseparable relationsip of the part to the whole.It is this principle of oneness underlying all geometry that permeates the architecture of all form in its myriad diversity. This principle of interconnectedness, inseparability and union provides us with a continuous reminder of our relationsip to the whole, a blueprint for the mind to the sacred foundation of all things created.